Se dice que dos fracciones son heterogéneas cuando estas poseen distinto denominador, por lo cual se diferencian de las fracciones homogéneas, que si tienen el mismo denominador en común.
Si lo que queremos es realizar sumas o restas con fracciones heterogéneas lo que debemos hacer en primer lugar, es encontrar el común denominador, o sea hallar el mínimo común múltiplo MCM de todos los denominadores.
Luego de ello lo que se debe hacer es colocar el denominador común, dividimos entonces el común denominador entre el primer denominador y el resultado lo multiplicamos por el numerador. Repetimos la operación con cada una de las fracciones que tengamos. Por último se suman los resultados obtenidos y así finalizamos.
A veces no es necesario multiplicar entre si los denominadores, eso depende de las fracciones que tengamos. Veamos ahora una serie de ejemplos bastante sencillos.
EN LA SUMA
Sin hacer el MCM
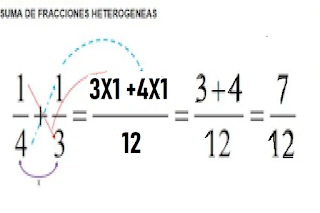
Para la suma de fracciones se puede utilizar la solución abreviada si se trata de operaciones simples como en el siguiente ejemplo:
En el ejemplo anterior referido a la suma de dos fracciones, se multiplican los denominadores y se obtiene como resultado 12. Luego ese valor se divide entre el denominador de la primera fracción 4 y se multiplica por el numerador de esa primera fracción que es 1. Quedaría en el numerador 3X1 .
Se realiza el mismo procedimiento para la segunda fracción, se divide el producto 12 entre el denominador de la segunda fracción 3 y se multiplica por el numerador de la segunda fracción que es 1. Quedaría
4 X 1 .
Luego ambos productos se suman en el numerador: 3X1 = 3 y 4x1= 4
Finalmente en el numerador quedará 3 + 4 = 7
Y en el denominador se mantendrá el producto de 4.3 (4x3) o sea 12
La respuesta será 7/12
Utilizando el MCM
En esta imagen se explica el procedimiento, se sobreentiende que el estudiante ya sabe lo que es el MCM.
Pero si aun no lo sabe o recuerda puede consultar nuestro post: ejemplos de MCM
Ejemplos sumar 2/3 + 3/4 utilizando el método del MCM
EN LA RESTA
En la resta o sustracción de fracciones heterogéneas debemos utilizar las mismas reglas que vimos en la suma, lo único que cambia es que en este caso tenemos que restar en vez de sumar. Veamos un par de ejemplos:
Sin MCM
Restar 3/4 - 5/7
En este caso, el procedimiento es similar a la suma, se multiplican los denominadores y el resultado, en este caso 28, se divide entre el denominador 4 de la primera fracción y el resultado 7 luego se multiplica por el numerador 3 de la primera fracción. 7x3.
Se hace lo mismo con la segunda fracción, se divide 28 entre el denominador 7 y luego el resultado 4 se multiplica por el numerador 5 de esta segunda fracción. 4x5.
Ambas multiplicaciones se ponen en el numerador y se restan como indica la imagen. El 28 del denominador se mantiene.
El resultado de 3/4 - 5/7 será entonces 21-20 /28 = 1/28
NOTA. Es importante recalcar lo que esta en rojo señalado en la imagen, en restas debe operarse el primer numerador siempre y luego el segundo. Es distinto , el caso de las sumas, podría hacerse en cualquier orden, puesto y el resultado sería igual, en cambio en la resta, si no se empieza por la primera fracción el resultado sería inexacto.
Utilizando el MCM
Restar 4/6 - 1/2
En este caso, en el que se utiliza el MCM se resuelve con el mismo procedimiento que con la suma.
-Se halla el MCM de los denominadores que es 6 como se indica en la imagen.
-Ese valor 6 se divide entre el denominador 6 de la primera fracción y el resultado 1 luego se multiplica por el numerador 4 de la primera fracción. 1x4 = 4
Se hace lo mismo con la segunda fracción, se divide 6 entre el denominador 2 y luego el resultado 3 se multiplica por el numerador 1 de esta segunda fracción. 3x1 = 3
Ambas multiplicaciones se ponen en el numerador y se restan como indica la imagen. El 6 del denominador se mantiene.
El resultado de 4/6 - 1/2 será entonces 4-3 /6 = 1/6
EN LA MULTIPLICACIÓN
En la multiplicación de fracciones, tanto fracciones homogéneas como heterogéneas se multiplican de igual forma.
El producto de dos o más fracciones es entonces igual a otra fracción que tiene como numerador el producto de los numeradores y tiene también como denominador el producto de los denominadores.
Veamos estos ejemplos:
EN LA DIVISIÓN Dividamos fracciones heterogéneas u homogéneas , debemos cambiar siempre a una multiplicación y la segunda fracción cambiará entonces a su recíproco. El cociente de dos fracciones será otra fracción que tendrá como numerador el producto del numerador de la primera por el denominador de la segunda y tendrá por denominador el producto del denominador de la primera multiplicado por el denominador de la segunda. Lo veremos claramente en los siguientes ejemplos:

EN LAS OPERACIONES COMBINADAS
Para el caso de ejercicios de operaciones combinadas de fracciones tomemos este ejemplo.
Buscar el resultado de 2/7 x 5/3 + 3/2 : 8/5
El resultado de la operación combinada
2/7 x 5/3 + 3/2 : 8/5 = 475 / 336
Recordemos que en operaciones combinadas primero se resuelve la multiplicación y división antes que la suma o resta. Y su hubiera paréntesis, se resuelve primero lo que está entre dicho paréntesis, empezando desde la izquierda si hay varios.






Publicar un comentario